Arquitetura de Estruturas

Descrição dos Materiais

Sistema e dessalinização

O sistema de salinização de água é crucial para transformar água salgada em água potável, atendendo à crescente demanda por recursos hídricos em áreas costeiras ou regiões com escassez de água doce. Este processo, essencial para garantir o acesso à água potável, envolve a remoção de sais e impurezas da água, tornando-a segura para consumo. O sistema de salinização proposto é composto por quatro estágios de filtragem, que garantem uma purificação eficiente e eficaz.

O estágio de filtragem possui três filtros: o filtro de polipropileno, que retém partículas grandes e impurezas visíveis, seguido pelo filtro de carvão ativado, que elimina cloro, substâncias químicas e compostos orgânicos, melhorando o sabor e odor da água. O filtro de resina mista vem em seguida, removendo metais pesados e outros contaminantes. O último estágio conta com uma membrana osmótica, que realiza a remoção dos sais e outras partículas dissolvidas na água por meio de um processo de osmose reversa. Para garantir a circulação contínua da água através desse sistema de filtragem, uma bomba d'água é utilizada para manter o fluxo e pressão ideais, assegurando o funcionamento eficiente e a purificação da água.

Com esse conjunto de tecnologias, o sistema proporciona uma solução eficaz para a obtenção de água potável, contribuindo para a sustentabilidade e a segurança hídrica.

Circuito Hidráulico

O circuito hidráulico, apresentado na imagem abaixo, desmonstra o trajeto do sistema de água desde a sua entrada. Os componentes ilustrados serão comentados de forma mais detalhada nos tópicos abaixo.

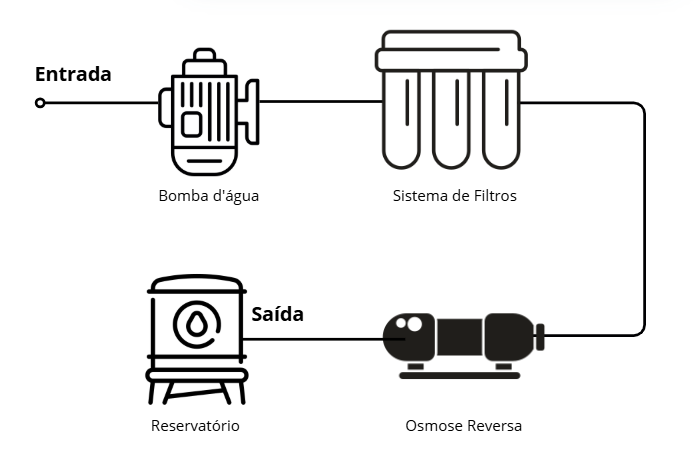
Materias

Para a construção do dessalinizador foram utilizados filtros comerciais, bomba d´água de alta pressão, um reservatorio de água, e uma gaiola de metal onde o sistema ficará acomodado. Estes descritos detalhadamente abaixo.

Filtros

Como dito anteriormente o sistema de dessalinização será composto por quatro estágios, filtros de polipropileno, carvão ativado e resina mista, mais uma membrana osmotica. A sequencia de filtragem corresponde a ordem postulada. E os filtros são componentes comerciais que seguem as diretrizes e normas do INMETRO (ASME B16.34, ASME VIII-1)

Filtro de polipropileno

Este filtro é ideal para filtração da água, com a finalidade de retenção de partículas sólidas como areia, barro, limo ou grãos de impurezas. O conjunto escolhido já veem com o elemento filtrante e carcaça.

Dimensões e parametros:

Elemento filtrante de Polipropileno Liso, 10” x 2 ½”
Diâmetro interno: 28mm
Diâmetro externo: 63,5mm
Vazão: até 1000 litros por hora
5 micras
Altura da carcaça (medidas externa): 33 cm
Diâmetro da carcaça (medidas externa): 12 cm
Material da carcaça: 100% policarbonato
Temperatura máxima de trabalho: até 60°C
Pressão máxima de trabalho: até 7 Kgf/cm²
Conexão de entrada e saída: rosca 3/4"
Compatível com filtros cartucho modelo: 10" x 2 1/2"

Dados obtidos a partir do site e fornecedora Liquid Filtros

Filtro de Carvão Ativado

A Filtração com Carvão Ativado, CarboBlock bloco de carvão tem como característica principal a absorção para redução de cloro, turbidez, cor, e odor de produtos orgânicos dissolvidos na água.

Dimensões e parametros:

Meio Filtrante Carvão ativado em bloco ou granulado.
Corpo e fechamento polipropileno.
Vedação BunaN
Temp. Trabalho até 60C.
Grau de filtração 5 micras.
Pressão máxima de trabalho até 7 Kgfcm.
Fabricado 100 com carvão ativado. Retenção de cloro 75
Fluxo máximo de água 300 litroshora

Dados obtidos a partir do site e fornecedora Filterinter

Filtro de Resina Mista

A resina mista é utilizada para desmineralização da água, com a finalidade de retenção de ions positivo e negativo. O processo de troca iônica baseia-se no emprego de resinas sintéticas, onde as mesmas retem os sais dissolvidos na água por meio de uma reação química, liberando íons equivalentes para água.

Dimensões e parametros:

Carcaça transparente 10" x 2 1/2"
Cartucho deionizador 10" x 2 1/2"
Resina Mista MB478/475 380g/0,6L (As resinas mista Purolite MB475 e MB478 são composta de 50% resina catiônica e 50% resina aniônica)

Dados obtidos a partir do site e fornecedora Liquid Filtros

Membrana Osmótica

O princípio da osmose reversa é simples: quando a água salgada ou contaminada é pressionada contra a membrana, os compostos dissolvidos (como os sais) não conseguem passar por ela, enquanto as moléculas de água pura podem atravessar. O resultado é uma água significativamente purificada, com uma alta taxa de remoção de sais e outras impurezas.

Dimensões e parametros:

Membrana de Osmose Reversa de 100GPD
Rejeita amplo espectro de impurezas com precisão de filtração ultra-alta de 0,001
taxa de produção sob condições ideais 97%
Pressão máxima de trabalho 200 Psi (7 kgf/c m²)

A carcaça para membrana é fabricada em polipropileno atóxico, branco, aprovada pela NSF sob a norma 58, FDA e homologada pela WQA

Dados obtidos a partir do site e fornecedora Filterinter

Bomba D´água

A bomba de agua foi escolhida a partir de duas análises, a primeira feita a partir do dimensionamento da bomda de água e calculos de perda de carga, que levam em consideração a percurso da dagua e a pressão de trabalho dos filtros para uma boa eficiência e vazão, e a segunda a partir dos parametros estabelecidos em conjunto pelos grupos de eletônica e energia.

Dessa forma o modelo escolhido foi uma bomba d´água de 100 Psi, 12 Volts e 36w.

Reservatorio

Com capacidade máxima de 25 Litros, foi escolhido um reservatorio de água que irá armazenar a água dessalinizada. Foi realizada a aánalise e estipulou-se que para o ciclo de salinização temos eles feito em 2,5h , com produção de 8 litros por hora, totalizando 20 litros de agua dessalinizada por ciclo.

Estrutura metalica

Para conseguir ser algo modular, e acrescentando a praticidade de poder dispor no ambiente de forma que melhor se adequa, foi pensado uma geometria retangular que servirá se estrutura para filtros, bomba, e componentes eletrônicos, como mostrado na imagem abaixo.

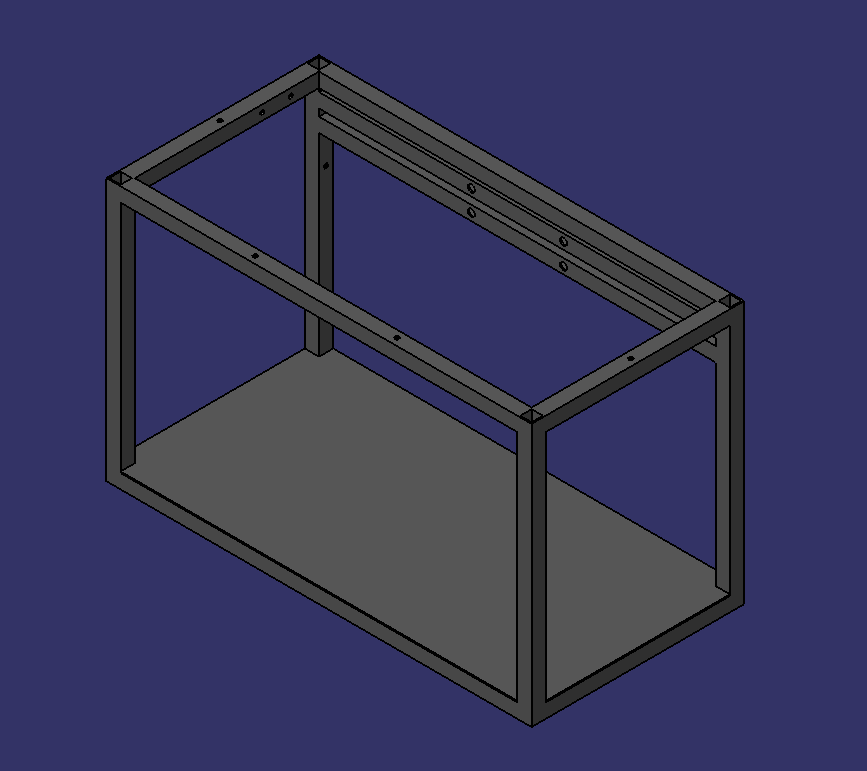
Ela será montada com barras de quadradas de perfil 20x20mm e uma espessura de 0.9mm. Esse material além de ser resistente a tensões aplicadas quando a estrutura for empilhada, também é facilmente encontrado em lojas de metalurgia, além de ser um material acessivel.

Calculo estrutural

Para atender os requisitos, a estrutura deve ser modular e com capacidade ser serem postas uma sobre a outra. Dessa forma fazemos algumas considerações iniciais, a carga sera uniformemente distribuida entras os 4 pilhares verticais que formam a nossa estrutura.

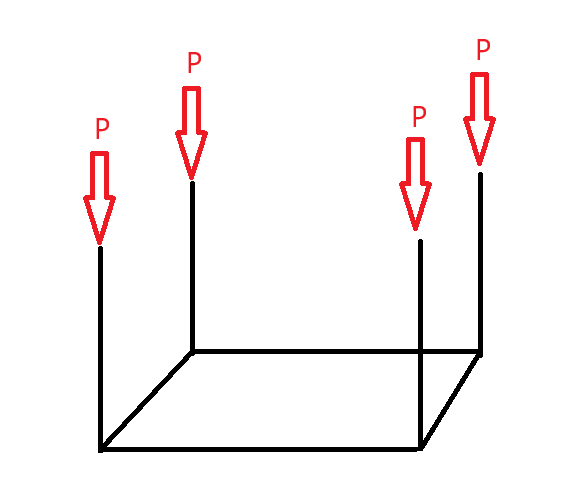
Inicialmente vemos qual a tensão em um pilar desses quanto a estrutura é posta sobre outra, considerando o peso de 25kg.

\[Peso_{Caixa} = 25kg * 9,81\frac{m}{s^2} = 245,25N\]

São 4 pilares logo a carga por pilar é:

\[ Carga_{pilar} = \frac{245,25N}{4} = 61,31N\]

A área da seção transversal de cada pilar será:

\[Área_{seção} = Área_{inteira} - Área_{vazia}\]

\[Área_{seção} = 20*20 - (20−2×0,9)(20−2×0,9) = 68,76mm^2\]

A carga máxima que cada pilar pode suportar, considerando o limite de escoamento de 250 MPa e um fator de segurança de 2, é dada por:

\[F_{max} = \frac{\sigma_0 * Área_{seção}}{FS}\]

Onde:

\[\sigma_0 = 250 MPa\]
\[Área_{seção} = 68,76mm^2\]
\[FS = 2\]

Logo:

\[F_{max} = 8595N\]

Agora, para saber quantas caixas podem ser empilhadas sem ultrapassar a carga máxima suportada, usamos a carga por pilar e dividimos pela carga que cada caixa exerce sobre um pilar.

\[N = \frac{8595N}{61,31N} = 140 caixas\]

Para validar os calculos, e as considerações, vamos fazer a analise númerica da geometria correta recorremos ao software ANSYS para a analise computacional, que utiliza de metodo de elementos finitos para os calculos.

Utilizando o modelo 3D feito, vemos que o peso de uma caixa, calculada anteriormente de 245,25N ficará distribuida na supericie superior por completa com a orientação voltada para a base.

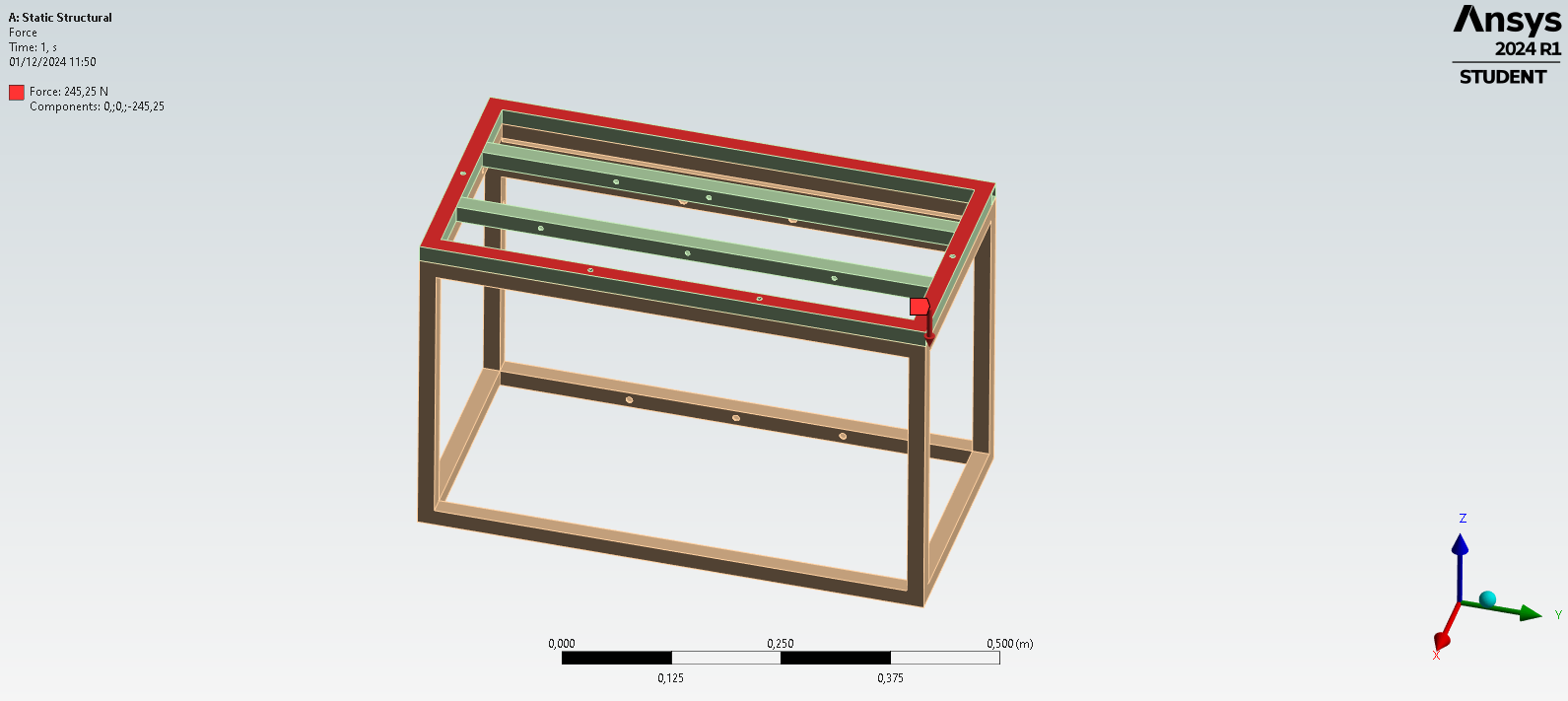
A malha refinada consta com 99931 nós e 49744 elementos.

Realizado a simulação temos o resultado:

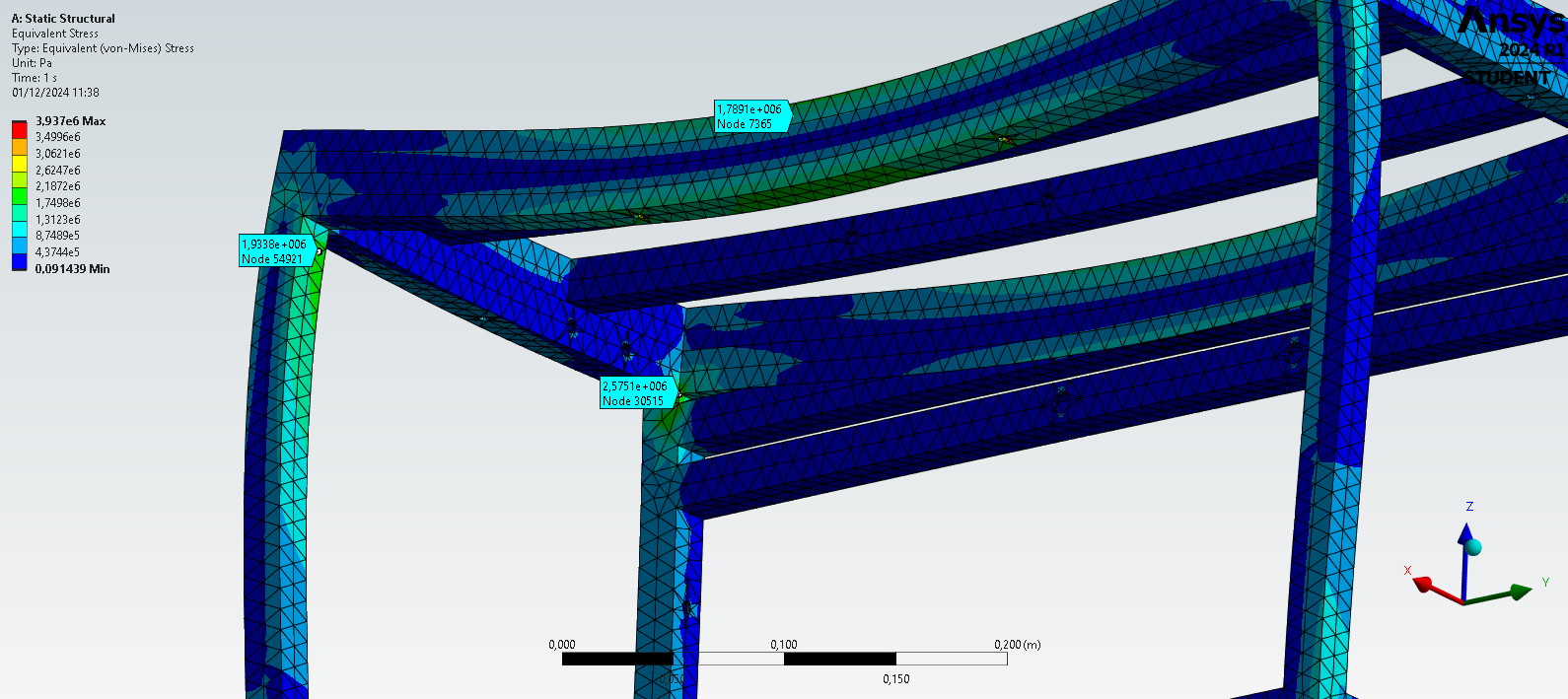
Vemos que p maior carregamento fica na estrutura superior nas vigas horizontais, e nos cantos de concentração de tensões, obtendo o valor maximo para tensão resultante, da aplicação de força de uma caixa sobreposta de 245,25N, de 3,93MPa.

Mantendo o mesmo fator de segurnça FS = 2. Podemos fazer os calculos de quantas caixas empilhadas a estrutura aguenta.

\[\sigma' = 3,93MPa * 2 = 7,86 MPa \]

Logo o numero de caixas que podem ser empilhas se dá pela razão da tensão de escoamento pela maxima tensão sofrida: \(\(N = \frac{\sigma_{0}}{\sigma'} = \frac{250MPa}{7,86MPa} = 31 caixas\)\)

Logo o maximo de estruturas que podem ser postas umas sobre as outras são 31 caixas completas com o sistema de filtragem.

Dimensionamento da Bomba

O dimensionamento em mecânica é o processo de definição das dimensões e especificações de peças e sistemas mecânicos para poderem suportar as cargas aplicadas e operar com segurança e eficiência. Este processo inclui cálculos de resistência dos materiais e a seleção adequada de materiais considerando os requisitos de cada aplicação. Além disso, fatores como vida útil, peso e custo são analisados para garantir ótimo desempenho e segurança dos componentes durante a operação.

Dimensionamento de Bomba d'água

As bombas são dispositivos que cedem parte da energia de uma fonte motora a um fluido, a fim de transportá-lo de um ponto a outro. Esta energia pode fornecida através do aumento de velocidade, pressão ou ambos.

Perda de Carga do Sistema

Durante o fluxo, o fluido entra em atrito com a parede do tubo, resultando em perda de pressão (hf), que se refere à energia perdida pelo fluido por unidade de massa. Os acessórios utilizados, como conexões, válvulas, redutores e outros, também influenciam na perda de pressão. Dessa forma, podemos dividi-la em duas partes: perda de carga distribuída (hfr), que é a perda em trechos retos; e perda de carga local (hfl), que é a perda que ocorre no acessório. Assim como mostra Equação 1:

\[hf = hfr + hfl \tag{1} \]

Como a perda de carga distribuída irá depender do tipo de escoamento (laminar ou turbulento).

Escoamentos de Fluidos, Número de Reynolds e Fator de Atrito

Escoamento Laminar:

Ocorre quando as partículas de um fluido movem-se ao longo de trajetórias bem definidas, tendendo a percorrer trajetórias paralelas, apresentando lâminas ou camadas e tendo cada uma delas a sua característica preservada no meio. No escoamento laminar a viscosidade age no fluido no sentido de amortecer a tendência de surgimento da turbulência.

Escoamento Turbulento:

Ocorre quando as partículas de um fluido não se movem ao longo de trajetórias bem definidas, ou seja, as partículas descrevem trajetórias irregulares, formando minúsculos redemoinhos ou vórtex.

Número de Reynolds:

O número de Reynolds é um número adimensional, usado em mecânica dos fluidos, que caracteriza o comportamento global de um fluido. A partir dele, podemos determinar a natureza do escoamento (laminar ou turbulento) dentro de um tubo ou sobre uma superfície.

Para o escoamento em tubos, o número de Reynolds é calculado da seguinte forma da equação 2:

\[Re=\frac{\rho Vd}{\mu}\tag{2} \]

Sendo;

ρ: Massa específica do fluido

V: Velocidade de escoamento do fluido

d: Diâmetro interno do tubo

μ: Viscosidade absoluta

E para determinarmos o tipo de escoamento, os seguintes critérios são seguidos:

Re < 2000 – Escoamento Laminar

2000 < Re < 4000 - Escoamento Transitório

Re > 4000 – Escoamento Turbulento

Fator de Atrito:

O fator de atrito f é função do número de Reynolds e da rugosidade relativa \(\varepsilon\)/D da tubulação, onde \(\varepsilon\) é a rugosidade e D é o diâmetro do tubo. Isso é válido exceto quando o escoamento é laminar, onde f depende apenas de Re; e no escoamento completamente turbulento, para o qual os valores de Reynolds são bastante altos e f passa a depender somente da rugosidade relativa

O valor da rugosidade do tubo pode ser obtido em tabelas que o informam de acordo com o material utilizado.

Perda de Carga Distribuída

A perda de carga distribuída pode ser expressa como a perda de pressão devido ao atrito do fluido com as paredes do tubo, geralmente representa a maior parcela da perda de energia pelo fluido numa tubulação.

Perda de Carga Distribuída no Escoamento Laminar

Podemos calcular a perda de carga distribuída no escoamento laminar utilizando a equação da de Darcy-Weisbach:

\[Re=f\frac{L}{d}\frac{ V^2}{ 2g}\tag{3} \]

Perda de Carga Localizada

A perda de carga localizada é definida como a perda de energia por unidade de peso que ocorre nos acessórios, tais como válvulas, curvas, retenções, filtros etc. Para sistemas pequenos com muitos acessórios, a perda localizada pode até exceder a perda distribuída.

O cálculo da perda de carga localizada pode ser feito usando essa fórmula da equação 4.

\[ℎ𝑓r=k\frac{ V^2}{ 2g}\tag{4} \]

Onde K expressa a influência do atrito, do diâmetro e do comprimento referente ao acessório utilizado. Os valores de K são tabelados e fornecidos pelos fabricantes.

A fórmula acima deve ser utilizada para cada acessório separadamente e então, depois, deve ser somada cada parcela da perda para que se possa obter a perda de carga localizada total.

Teorema de Bernoulli

O teorema de Bernoulli representa um caso particular do princípio da conservação de energia, expressando que num fluido ideal, a energia se conserva ao longo de seu percurso. A energia total de um fluido pode se apresentar das seguintes formas: energia de pressão, que é a energia do fluido devido à pressão que possui; energia cinética, que é a energia devido à velocidade do fluido e a energia potencial gravitacional, que é a energia devido à altura que se encontra o fluido.

A energia de pressão por unidade de peso em um determinado ponto do fluido é definida como:

\[E_{p}=\frac{ P}{ \gamma}\tag{5} \]

Sendo:

P: a pressão atuante num ponto do fluido

ɣ: o peso específico do fluido.

A energia cinética por unidade de peso é definida como:

\[E_{c}=\frac{ V^2}{ 2g}\tag{6} \]

Sendo;

V: velocidade do fluido

g: aceleração da gravidade

A energia potencial gravitacional por unidade de peso em um ponto do fluido é definida como a cota (Z) deste ponto em relação a um determinado plano de referência.

Considerando-se um escoamento permanente e um fluido ideal, a energia total em qualquer ponto do fluido é constante e é dada pela soma das energias de pressão, cinética e potencial gravitacional. A expressão geral da equação 8 do Teorema de Bernoulli fica assim;

\[\frac{ P_{1}}{ \gamma}+\frac{ V^2_{1}}{ 2g} + z_{1} = \frac{ P_{2}}{ \gamma}+\frac{ V^2_{2}}{ 2g} + z_{2}\tag{8} \]

Solucionando

Utilizando-se a equação (8) da energia para escoamento permanente e colocando perdas e atrito. A equação fica assim:

\[\frac{ P_{1}}{ \gamma}+\frac{ V^2_{1}}{ 2g} + z_{1} = \frac{ P_{2}}{ \gamma}+\frac{ V^2_{2}}{ 2g} + z_{2} + h_{pd} + \sum h_{pl} + h_{B} \tag{9} \]

Em que \(h_{B}\) é o acréscimo de altura através da bomba. Mas, como pressão ambos lado são pressão atmosfera, portanto,\(P_{1}\) = \(P_{2}\).

A velocidade do fluido de entrada e saída aproxima de 0, assim \(V_{1}\) = \(V_{2}\) \(\approx\) 0. E altura do reservátorio é mesmo da bomba, portanto \(z_{2}\)=0. Colocando-se equação para a altura da bomba;

\[ h_{B}= z_{1} + h_{pd} + \sum h_{pl} \tag{10} \]

\[ h_{B}= 0,40m + \frac{ V^2}{ 2g} (\frac{ fL}{ d} + \sum K) \tag{11} \]

Considerando a vazão bomba de 4,5L/m que é igual \(7,5x10^{-5}\) \(m^3/s\). E diâmetro da entrada e da saída da bomba possui 6,5mm.

Calcule-se à velocidade;

\[v=\frac{Q}{A}\]

\[v=\frac{7,5x10^{-5}}{\frac{ \Pi }{ 4}(0,0065)^2}\]

\[v=2,26m/s\]

Os valores dos comprimentos equivalentes referentes a cada acessório foram utilizado na tabela (1)

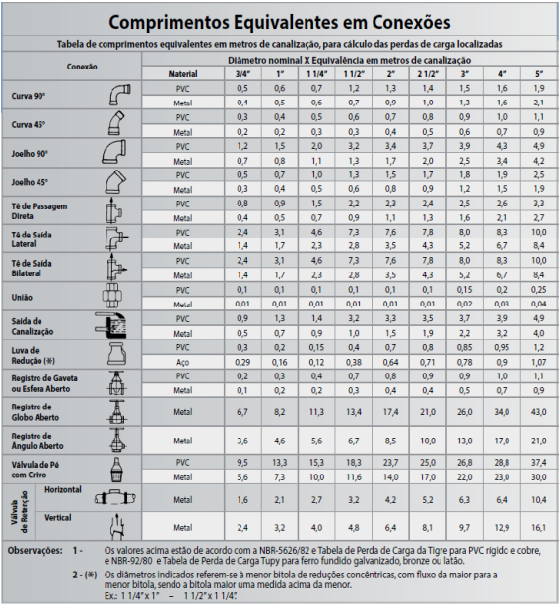
Com isso, foram listados os acessórios que vão ser utilizada no dimensionamento e respectivas valores do K, como mostra na tabela (2).

	Quantidades	K
Curva de 45º	19	0,3
Joelho de 90º	5	1,2
Filtro de sedimento	1	0,5
Filtro de carvão ativado	1	1,0
Membrana de osmose	1	3,0
Entrada e saída do tubo	2	1,0

Tabela 2 - Lista dos coeficientes de perda localizada.

\[\sum K=18,2\]

Os valores de k para os filtros de osmose reversa doméstica foram obtidos a partir de fontes técnicas, incluindo o Hydronix Water Technology, fabricante de sistemas de filtração, e o manual técnico DuPont FilmTec Reverse Osmosis and Nanofiltration Membrane Manual, que oferece orientações detalhadas sobre o desempenho e a perda de carga associada a membranas de osmose reversa.

Calcule-se o número de Reynolds e fator de atrito do tubo;

\[Re_{d}=\frac{vd}{\nu}\]

\[Re_{d}=\frac{2,26*0,0065d}{1,02*10^{-6}}\]

\[Re_{d}=14401,96\]

A rugosidade absoluta para PVC utilizou-se a figura (2)

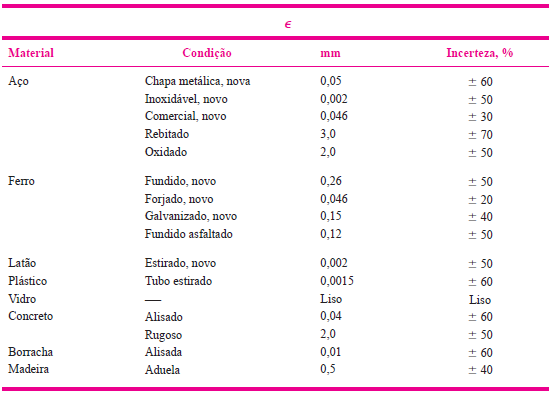
Figura 11: Valores recomendados de rugosidade para dutos comerciais.

Assim, calcule-se rugosidade adimensional para ser utilizada no diagrama de Moody da figura(3).

\[ \frac{\varepsilon }{D}=\frac{0,0015mm}{6,5mm}\]

\[\frac{\varepsilon }{D}=0,000231\]

Figura 10:O atrito em tubos com paredes lisas e rugosas.

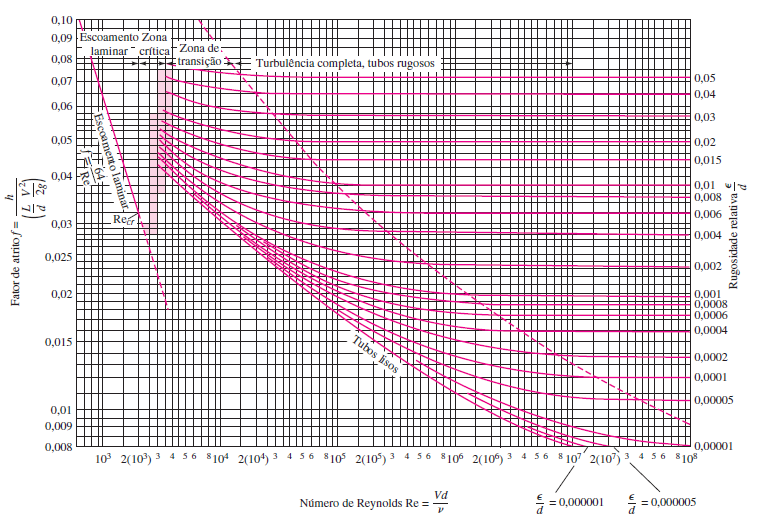
Consequentemente, o fator de atrito ficou \(f \approx 0,015\).

Substituindo na Equação (11)

\[ h_{B}= 0,40m + \frac{ V2,26^2}{ 2*9,81} (\frac{ 0,015*15}{ 0,0065} + 18,2) \]

\[ h_{B}= 14,15\]

A bomba deve fornecer uma potência hidráulica;

\[P=\rho gQh_{B}\]

\[P=1000*9,81*7,5*10^{-5}*14,15\]

\[P=10,41 w \]

Considerando um rendimento da bomba d'água entre 40% a 60%, adotou-se \(\eta = 0,4\). Esse valor foi escolhido com base nas condições operacionais típicas da bomba.

\[ \eta =\frac{P_{hidráulica}}{P_{consumida}} \]

\[P_{con}=26 w \]

Logo, a potência mínima instalada neste projeto deve ser superior a 26 W. Consequentemente, qualquer valor de potência acima desse valor será adequado para atender às necessidades do projeto.

Histórico de versão

Data	Versão	Descrição	Autores	Revisor
27/11/2024	1.0	Construção do Documento	Giovanna Palheta
30/11/2024	2.0	Simulação e cálculo estrutural	Arthur Rodrigues
01/12/2024	2.1	Simulação atualizada	Arthur Rodrigues	Mylena
31/01/2024	3.0	Circuito Hidráulico	Giovanna Palheta